In deep learning, classification models don’t just need to make predictions—they need to express confidence. That’s where the Softmax activation function comes in. Softmax takes the raw, unbounded scores produced by a neural network and transforms them into a well-defined probability distribution, making it possible to interpret each output as the likelihood of a specific class. 

This property makes Softmax a cornerstone of multi-class classification tasks, from image recognition to language modeling. In this article, we’ll build an intuitive understanding of how Softmax works and why its implementation details matter more than they first appear. Check out the .

Implementing Naive Softmax

import torch

def softmax_naive(logits):
    exp_logits = torch.exp(logits)
    return exp_logits / exp_logits.sum(dim=1, keepdim=True)

This function implements the Softmax activation in its most straightforward form. It exponentiates each logit and normalizes it by the sum of all exponentiated values across classes, producing a probability distribution for each input sample. 

While this implementation is mathematically correct and easy to read, it is numerically unstable—large positive logits can cause overflow, and large negative logits can underflow to zero. As a result, this version should be avoided in real training pipelines. Check out the .

Sample Logits and Target Labels

This example defines a small batch with three samples and three classes to illustrate both normal and failure cases. The first and third samples contain reasonable logit values and behave as expected during Softmax computation. The second sample intentionally includes extreme values (1000 and -1000) to demonstrate numerical instability—this is where the naive Softmax implementation breaks down. 

The targets tensor specifies the correct class index for each sample and will be used to compute the classification loss and observe how instability propagates during backpropagation. Check out the .

# Batch of 3 samples, 3 classes
logits = torch.tensor([
    [2.0, 1.0, 0.1],      
    [1000.0, 1.0, -1000.0],  
    [3.0, 2.0, 1.0]
], requires_grad=True)

targets = torch.tensor([0, 2, 1])

Forward Pass: Softmax Output and the Failure Case

During the forward pass, the naive Softmax function is applied to the logits to produce class probabilities. For normal logit values (first and third samples), the output is a valid probability distribution where values lie between 0 and 1 and sum to 1. 

However, the second sample clearly exposes the numerical issue: exponentiating 1000 overflows to infinity, while -1000 underflows to zero. This results in invalid operations during normalization, producing NaN values and zero probabilities. Once NaN appears at this stage, it contaminates all subsequent computations, making the model unusable for training. Check out the .

# Forward pass
probs = softmax_naive(logits)

print("Softmax probabilities:")
print(probs)

Target Probabilities and Loss Breakdown

Here, we extract the predicted probability corresponding to the true class for each sample. While the first and third samples return valid probabilities, the second sample’s target probability is 0.0, caused by numerical underflow in the Softmax computation. When the loss is calculated using -log(p), taking the logarithm of 0.0 results in +∞. 

This makes the overall loss infinite, which is a critical failure during training. Once the loss becomes infinite, gradient computation becomes unstable, leading to NaNs during backpropagation and effectively halting learning. Check out the .

# Extract target probabilities
target_probs = probs[torch.arange(len(targets)), targets]

print("nTarget probabilities:")
print(target_probs)

# Compute loss
loss = -torch.log(target_probs).mean()
print("nLoss:", loss)

Backpropagation: Gradient Corruption

When backpropagation is triggered, the impact of the infinite loss becomes immediately visible. The gradients for the first and third samples remain finite because their Softmax outputs were well-behaved. However, the second sample produces NaN gradients across all classes due to the log(0) operation in the loss. 

These NaNs propagate backward through the network, contaminating weight updates and effectively breaking training. This is why numerical instability at the Softmax–loss boundary is so dangerous—once NaNs appear, recovery is nearly impossible without restarting training. Check out the .

loss.backward()

print("nGradients:")
print(logits.grad)

Numerical Instability and Its Consequences

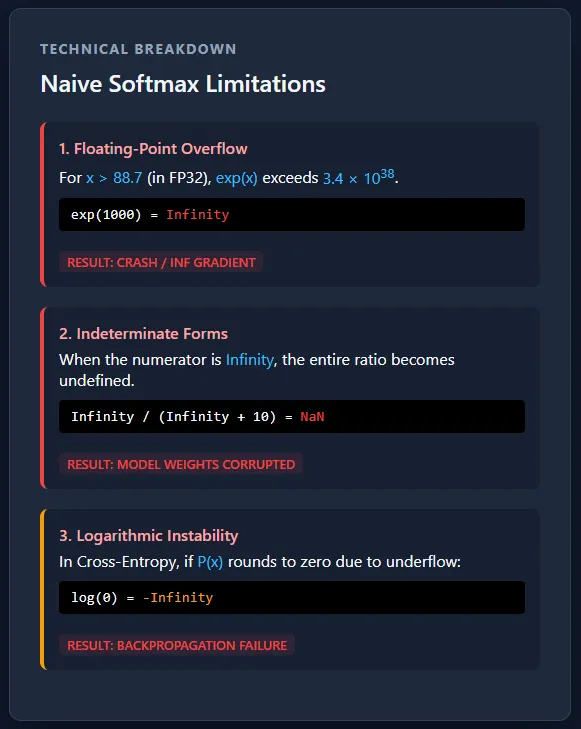
Separating Softmax and cross-entropy creates a serious numerical stability risk due to exponential overflow and underflow. Large logits can push probabilities to infinity or zero, causing log(0) and leading to NaN gradients that quickly corrupt training. At production scale, this is not a rare edge case but a certainty—without stable, fused implementations, large multi-GPU training runs would fail unpredictably. 

The core numerical problem comes from the fact that computers cannot represent infinitely large or infinitely small numbers. Floating-point formats like FP32 have strict limits on how big or small a value can be stored. When Softmax computes exp(x), large positive values grow so fast that they exceed the maximum representable number and turn into infinity, while large negative values shrink so much that they become zero. Once a value becomes infinity or zero, subsequent operations like division or logarithms break down and produce invalid results. Check out the .

Implementing Stable Cross-Entropy Loss Using LogSumExp

This implementation computes cross-entropy loss directly from raw logits without explicitly calculating Softmax probabilities. To maintain numerical stability, the logits are first shifted by subtracting the maximum value per sample, ensuring exponentials stay within a safe range. 

The LogSumExp trick is then used to compute the normalization term, after which the original (unshifted) target logit is subtracted to obtain the correct loss. This approach avoids overflow, underflow, and NaN gradients, and mirrors how cross-entropy is implemented in production-grade deep learning frameworks. Check out the .

def stable_cross_entropy(logits, targets):

    # Find max logit per sample
    max_logits, _ = torch.max(logits, dim=1, keepdim=True)

    # Shift logits for numerical stability
    shifted_logits = logits - max_logits

    # Compute LogSumExp
    log_sum_exp = torch.log(torch.sum(torch.exp(shifted_logits), dim=1)) + max_logits.squeeze(1)

    # Compute loss using ORIGINAL logits
    loss = log_sum_exp - logits[torch.arange(len(targets)), targets]

    return loss.mean()

Stable Forward and Backward Pass

Running the stable cross-entropy implementation on the same extreme logits produces a finite loss and well-defined gradients. Even though one sample contains very large values (1000 and -1000), the LogSumExp formulation keeps all intermediate computations in a safe numerical range. As a result, backpropagation completes successfully without producing NaNs, and each class receives a meaningful gradient signal. 

This confirms that the instability seen earlier was not caused by the data itself, but by the naive separation of Softmax and cross-entropy—an issue fully resolved by using a numerically stable, fused loss formulation. Check out the .

logits = torch.tensor([
    [2.0, 1.0, 0.1],
    [1000.0, 1.0, -1000.0],
    [3.0, 2.0, 1.0]
], requires_grad=True)

targets = torch.tensor([0, 2, 1])

loss = stable_cross_entropy(logits, targets)
print("Stable loss:", loss)

loss.backward()
print("nGradients:")
print(logits.grad)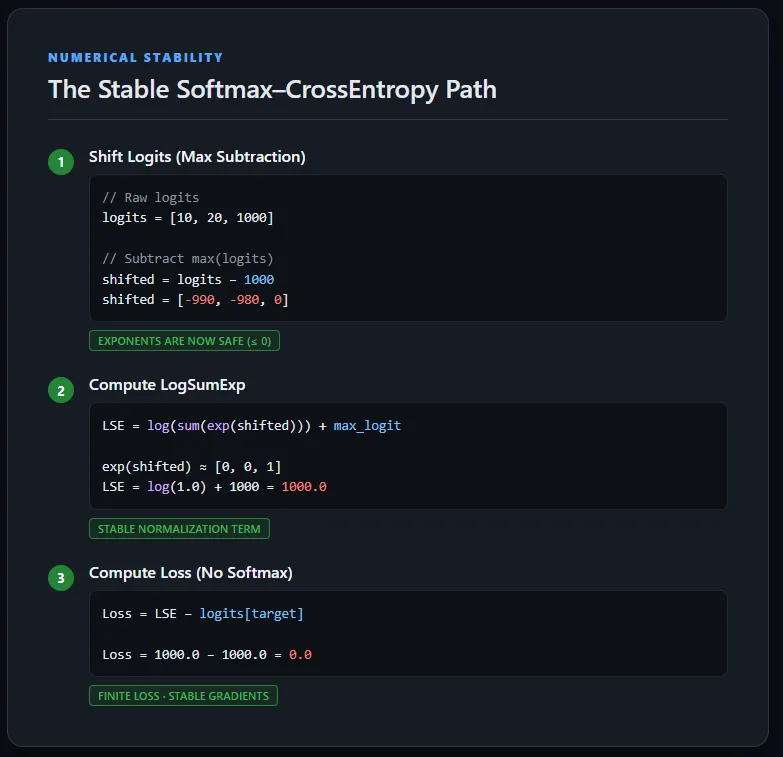

Conclusion

In practice, the gap between mathematical formulas and real-world code is where many training failures originate. While Softmax and cross-entropy are mathematically well-defined, their naive implementation ignores the finite precision limits of IEEE 754 hardware, making underflow and overflow inevitable. 

The key fix is simple but critical: shift logits before exponentiation and operate in the log domain whenever possible. Most importantly, training rarely requires explicit probabilities—stable log-probabilities are sufficient and far safer. When a loss suddenly turns into NaN in production, it’s often a signal that Softmax is being computed manually somewhere it shouldn’t be.

Check out the . Also, feel free to follow us on  and don’t forget to join our  and Subscribe to . Wait! are you on telegram? 

Check out our latest release of , a 2025-focused analytics platform that turns model launches, benchmarks, and ecosystem activity into a structured dataset you can filter, compare, and export

The post appeared first on .