DeepSeek researchers are trying to solve a precise issue in large language model training. Residual connections made very deep networks trainable, hyper connections widened that residual stream, and training then became unstable at scale. The new method mHC, Manifold Constrained Hyper Connections, keeps the richer topology of hyper connections but locks the mixing behavior on a well defined manifold so that signals remain numerically stable in very deep stacks.

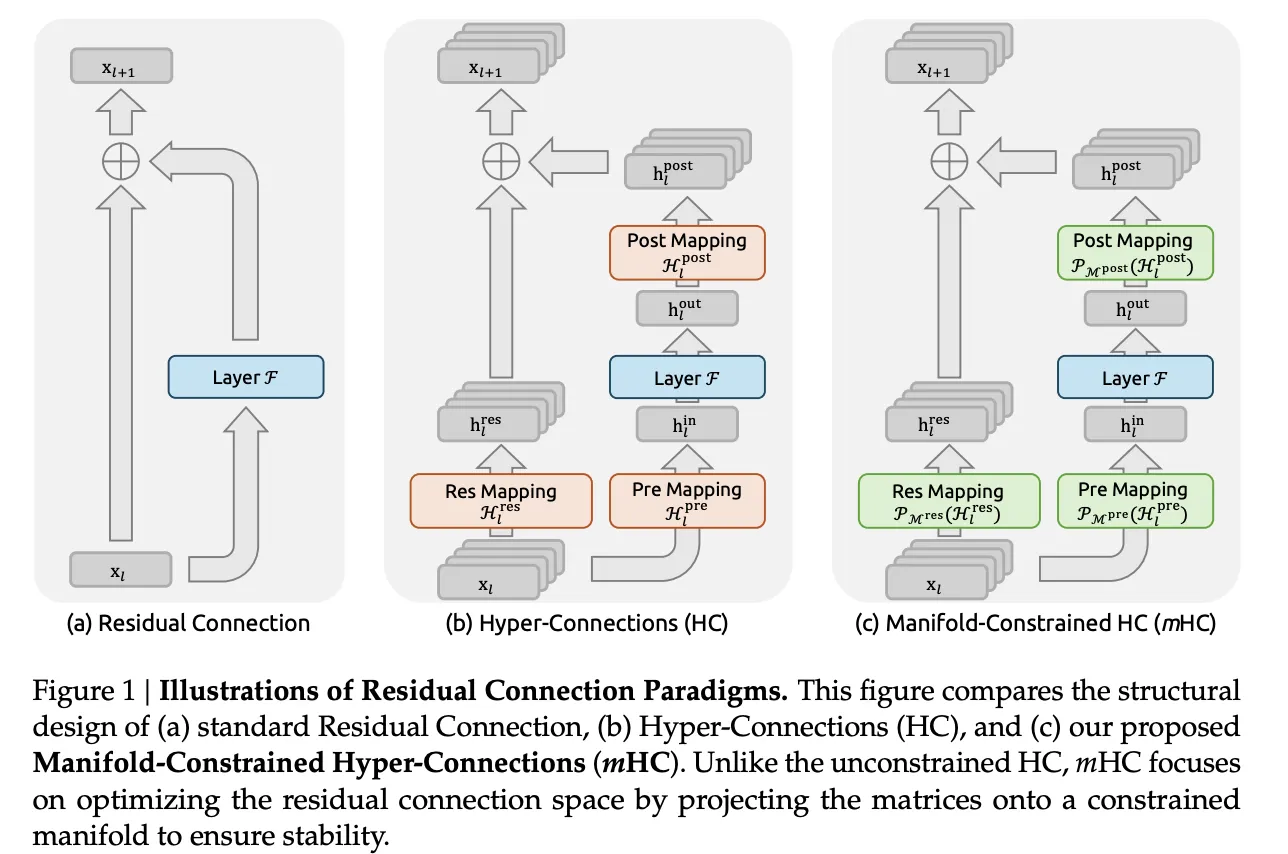
From Residual Connections To Hyper Connections

Standard residual connections, as in ResNets and Transformers, propagate activations with x_l+1​=x_l​+F(x_l​,W_l​)
The identity path preserves magnitude and keeps gradients usable even when you stack many layers.

Hyper Connections generalize this structure. Instead of a single residual vector of size C, the model keeps an n stream buffer 𝑥_𝑙∈𝑅^𝑛×𝐶. Three learned mappings control how each layer reads and writes this buffer:

• H_l^pre selects a mixture of streams as the layer input
• F is the usual attention or feed forward sublayer
• H_l^post writes results back into the n stream buffer
• H_l^res​∈R^n×n mixes streams between layers

The update has the form
x_l+1​=H_l^res​x_l​+H_l^post​^⊤F(H_l^pre​x_l​,W_l​)

With n set to 4, this design increases expressivity without a large increase in floating point cost, which is why hyper connections improve downstream performance in language models.

Why Hyper Connections Become Unstable

The problem appears when you look at the product of residual mixers across many layers. In a 27B mixture of experts model, DeepSeek studies the composite mapping

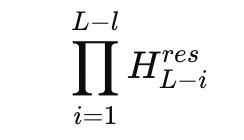
and defines an Amax Gain Magnitude based on maximum row and column sums. This metric measures worst case amplification in the forward and backward signal paths. In the hyper connection model, this gain reaches peaks around 3000, far from the ideal value 1 that you expect from a stable residual path.

This means small per layer deviations compound into very large amplification factors across depth. Training logs show loss spikes and unstable gradient norms relative to a baseline residual model. At the same time, keeping a multi stream buffer increases memory traffic for each token, which makes naive scaling of hyper connections unattractive for production large language models.

Manifold Constrained Hyper Connections

mHC keeps the multi stream residual idea but constrains the dangerous part. The residual mixing matrix H_l^res no longer lives in the full n by n space. Instead, it is projected onto the manifold of doubly stochastic matrices, also called the Birkhoff polytope. In that set all entries are non negative and each row and each column sums to 1.

DeepSeek team enforces this constraint with the classical Sinkhorn Knopp algorithm from 1967, which alternates row and column normalizations to approximate a doubly stochastic matrix. The research team uses 20 iterations per layer during training, which is enough to keep the mapping close to the target manifold while keeping cost manageable.

Under these constraints, H_l^res​x_l behaves like a convex combination of residual streams. Total feature mass is preserved and the norm is tightly regularized, which eliminates the explosive growth seen in plain hyper connections. The research team also parameterize input and output mappings so that coefficients are non negative, which avoids cancellation between streams and keeps the interpretation as averaging clear.

With mHC the composite Amax Gain Magnitude stays bounded and peaks at about 1.6 in the 27B model, compared with peaks near 3000 for the unconstrained variant. That is a reduction of about 3 orders of magnitude in worst case amplification, and it comes from a direct mathematical constraint rather than tuned tricks.

Systems Work And Training Overhead

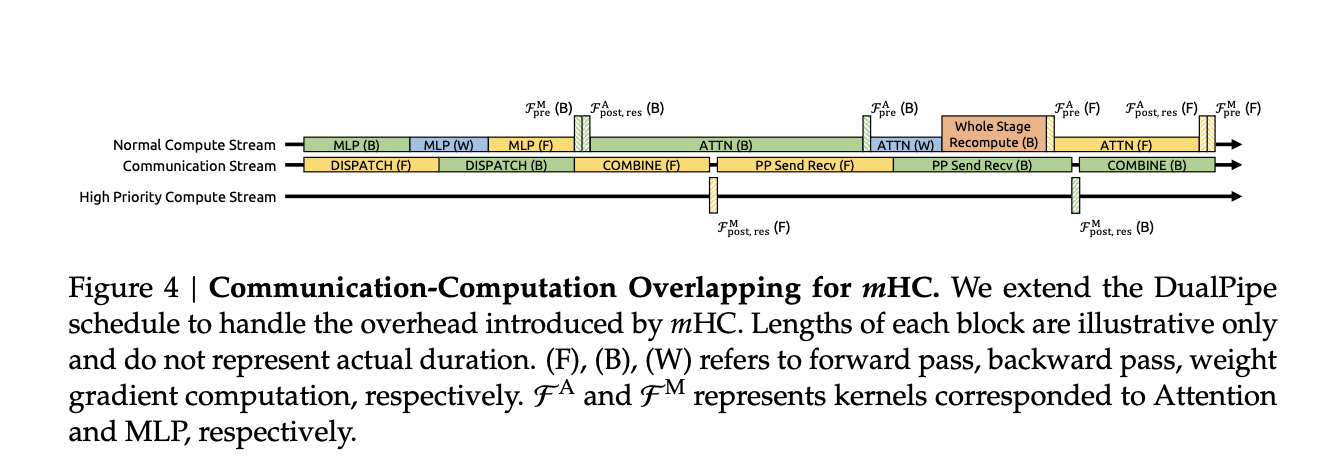
Constraining every residual mixer with Sinkhorn style iterations adds cost on paper. The research team addresses this with several systems choices:

• Fused kernels combine RMSNorm, projections and gating for the mHC mappings so that memory traffic stays low
• Recompute based activation checkpointing trades compute for memory by recomputing mHC activations during backprop for blocks of layers
• Integration with a DualPipe like pipeline schedule overlaps communication and recomputation, so that additional work does not stall the training pipeline

In large scale in house training runs, mHC with expansion rate n equal to 4 adds about 6.7 percent training time overhead relative to the baseline architecture. That figure already includes both the extra compute from Sinkhorn Knopp and the infrastructure optimizations.

Empirical Results

The research team trains 3B, 9B and 27B mixture of experts models and evaluates them on a standard language model benchmark suite, including tasks like BBH, DROP, GSM8K, HellaSwag, MMLU, PIQA and TriviaQA.

For the 27B model, the reported numbers on a subset of tasks show the pattern clearly:

• Baseline: BBH 43.8, DROP F1 47.0
• With hyper connections: BBH 48.9, DROP 51.6
• With mHC: BBH 51.0, DROP 53.9

So hyper connections already provide a gain over the basic residual design, and manifold constrained hyper connections push performance further while restoring stability. Similar trends appear on other benchmarks and across model sizes, and scaling curves suggest that the advantage persists across compute budgets and through the full training trajectory rather than only at convergence.

Key Takeaways

• mHC stabilizes widened residual streams: mHC, Manifold Constrained Hyper Connections, widens the residual pathway into 4 interacting streams like HC, but constrains the residual mixing matrices on a manifold of doubly stochastic matrices, so long range propagation remains norm controlled instead of exploding.
• Exploding gain is reduced from ≈3000 to ≈1.6: For a 27B MoE model, the Amax Gain Magnitude of the composite residual mapping peaks near 3000 for unconstrained HC, while mHC keeps this metric bounded around 1.6, which removes the exploding residual stream behavior that previously broke training.
• Sinkhorn Knopp enforces doubly stochastic residual mixing: Each residual mixing matrix is projected with about 20 Sinkhorn Knopp iterations so that rows and columns both sum to 1, making the mapping a convex combination of permutations, which restores an identity like behavior while still allowing rich cross stream communication.
• Small training overhead, measurable downstream gains: Across 3B, 9B and 27B DeepSeek MoE models, mHC improves benchmark accuracy, for example about plus 2.1 percent on BBH for the 27B model, while adding only about 6.7 percent training time overhead through fused kernels, recompute and pipeline aware scheduling.
• Introduces a new scaling axis for LLM design: Instead of only scaling parameters or context length, mHC shows that explicitly designing the topology and manifold constraints of the residual stream, for example residual width and structure, is a practical way to unlock better performance and stability in future large language models.

---

Check out the  Also, feel free to follow us on  and don’t forget to join our  and Subscribe to . Wait! are you on telegram? 

The post appeared first on .